[Flight Control 5] - Aircraft Equation of Angular Motion

Aircraft Equations of Motion

Law of Conservation of Angular Momentum

뉴턴의 제 2 법칙을 기반으로 회전 운동량(Angular Momentum) 보존법칙은 다음과 같이 표현된다.

\[\Sigma M_i = \frac{d}{dt} (H) \tag{1}\]

또한, 이 식은 아래와 같은 의미를 가진다.

• “회전 운동량의 시간 변화율은 항공기에 작용하는 외부 모멘트의 총합과 같다.”

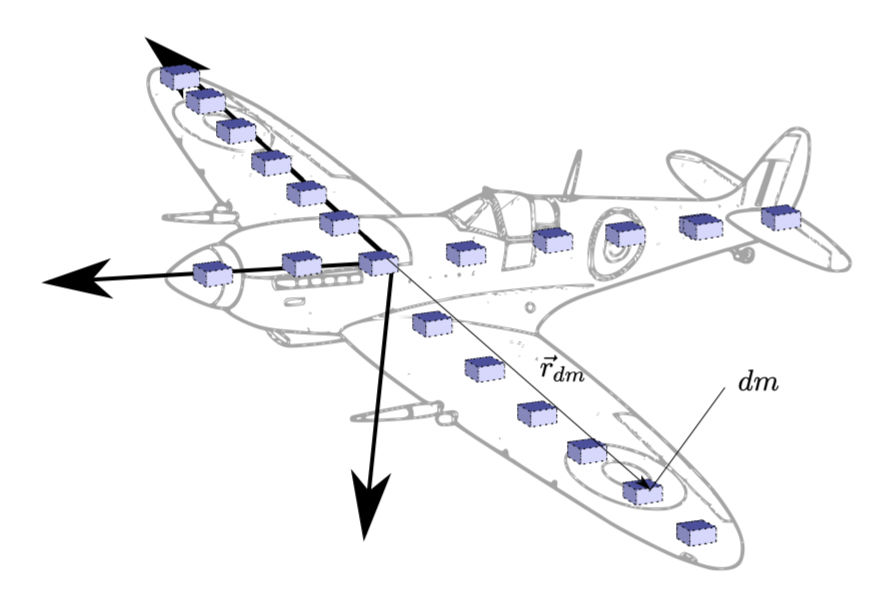
강체인 항공기에 대해 회전 운동량은 다음과 같이 정의된다.

\[H = I \omega \tag{2}\]

Point Mass Model of the Aircraft

이때 관성 행렬 $I$는 다음과 같이 정의된다.

\[I = \begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{yx} & I_{yy} & -I_{yz} \\ -I_{zx} & -I_{zy} & I_{zz} \end{bmatrix} \tag{3}\]

여기서 $I_i$는 주 관성 모멘트(Principal Moment of Inertia)이고, $I_{ij} (i \neq j)$는 관성곱(Product of Inertia)이다.
주 관성 모멘트는 각 축에서 회전할 때의 관성을 뜻하며, 관성 곱은 하나의 축이 회전할 때 다른 축에 미치는 영향을 뜻한다.

\[I_{xx} = \int (y^2 + z^2) \rho \, dv, \quad I_{yz} = I_{zy} = \int yz \rho \, dv \tag{4}\] \[I_{yy} = \int (z^2 + x^2) \rho \, dv, \quad I_{zx} = I_{xz} = \int zx \rho \, dv \tag{5}\] \[I_{zz} = \int (x^2 + y^2) \rho \, dv, \quad I_{xy} = I_{yx} = \int xy \rho \, dv \tag{6}\]

Equation of Angular Motion

이전 포스트에서 다루었던 Equation of Linear Motion과 같이 Angular Motion에서도 기체 고정 좌표계에서의 운동을 정확하게 설명하기 위하여 식(7)과 같이 바꿔서 계산을 진행한다.

\[\frac{dH}{dt} = \frac{\delta H}{\delta t} + \omega \times H \tag{7}\]

항공기에 작용하는 공기역학적인 힘과 추진기관의 추력에 의해 항공기 무게중심에 작용하는 모든 모멘트를 고려하고, 회전 운동량 보존법칙인 식에 대입하면 식(8)을 도출할 수 있다.

\[\frac{\delta H}{\delta t} + \omega \times H = \sum M_i = M_A + M_T \tag{8}\]

먼저, 회전 운동량을 계산해 보면 식(9)와 같이 나온다.

\[H = \begin{bmatrix} h_x \\ h_y \\ h_z \end{bmatrix} = \begin{bmatrix} I_{xx} & - I_{xy} & - I_{xz} \\ - I_{yx} & I_{yy} & - I_{yz} \\ - I_{zx} & - I_{zy} & I_{zz} \end{bmatrix} \begin{bmatrix} P \\ Q \\ R \end{bmatrix} = \begin{pmatrix} I_{xx}P - I_{xy}Q - I_{xz}R \\ -I_{yx}P + I_{yy}Q - I_{yz}R \\ -I_{zx}P - I_{zy}Q + I_{zz}R \end{pmatrix} \tag{9}\]

항공기 동체 축 기준 벡터에 대하여 다음과 같이 표현할 수 있다.

\[H = h_x \hat{i} + h_y \hat{j} + h_z \hat{k} \tag{10}\]

Simplification of Aircraft Equations of Angular Motion

Symmetry of the Airplane in the XZ-plane

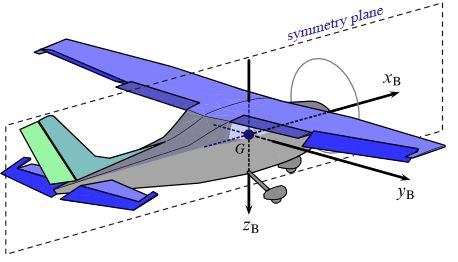
전형적인 항공기는 세로면(XZ-면)에 대칭으로 설계되고 제작된다.
이러한 좌우 대칭인 항공기 특성을 고려하면 관성모멘트에 대해서 다음 관계가 성립한다.

\[I_{xy} = I_{yx} = 0 \quad I_{yz} = I_{zy} = 0 \tag{11}\]

먼저, 회전 운동량을 표현하는 일반적인 식(12)~(14)은 다음과 같다.

\[h_x = I_{xx}P - I_{xy}Q - I_{xz}R \tag{12}\] \[h_y = -I_{yx}P + I_{yy}Q - I_{yz}R \tag{13}\] \[h_z = -I_{zx}P - I_{zy}Q + I_{zz}R \tag{14}\]

항공기의 대칭성을 고려하여 위 식들을 단순화한 결과는 식(15)~(17)과 같다.

\[h_x = I_{xx} P - I_{xz} R \tag{15}\] \[h_y = I_{yy} Q \tag{16}\] \[h_z = -I_{zx} P + I_{zz} R \tag{17}\]

또한, 시간에 대한 미분값과 회전 관성도 아래와 같이 단순화 할 수 있다.

\[\frac{\delta H}{\delta t} = (I_{xx} \dot{P} - I_{xz} \dot{R}) \hat{i} + I_{yy} \dot{Q} \hat{j} + (-I_{zx} \dot{P} + I_{zz} \dot{R}) \hat{k} \tag{18}\] \[\omega \times H = (Q h_z - R h_y) \hat{i} + (R h_x - P h_z) \hat{j} + (P h_y - Q h_x) \hat{k} \tag{19}\] \[M_A = L_A \hat{i} + M_A \hat{j} + N_A \hat{k} \quad M_T = L_T \hat{i} + M_T \hat{j} + N_T \hat{k} \tag{20}\]

위의 관계식을 모두 회전 운동량 보존식에 대입해보면

\[\begin{aligned} & {I_{xx} \dot{P} - I_{xz} \dot{R} + Q R (I_{zz} - I_{yy}) - PQ I_{xz} }\hat{i} \\ & + \{ I_{yy} \dot{Q} + PR (I_{xx} - I_{zz}) + (P^2 - R^2) I_{xz} \} \hat{j} \\ & + \{ I_{zz} \dot{R} - I_{xz} \dot{P} + PQ (I_{yy} - I_{xx}) + QRI_{xz} \} \hat{k} \\ & = (L_A + L_T) \hat{i} + (M_A + M_T) \hat{j} + (N_A + N_T) \hat{k} \end{aligned} \tag{21}\]

결과적으로 다음 3개의 방정식을 얻게 된다.

\[I_{xx} \dot{P} - I_{xz} \dot{R} - I_{xz} PQ + (I_{zz} - I_{yy}) QR = L_A + L_T \tag{22}\] \[I_{yy} \dot{Q} + (I_{xx} - I_{zz}) PR + I_{xz} (P^2 - R^2) = M_A + M_T \tag{23}\] \[I_{zz} \dot{R} - I_{xz} \dot{P} + (I_{yy} - I_{xx}) PQ + I_{xz} QR = N_A + N_T \tag{24}\]

이로서, 우리는 항공기의 운동을 모두 표현할 수 있는 선형 운동방정식 및 회전 운동방정식까지 모두 도출하였다.