[Flight Control 4] - Aircraft Equation of Linear Motion

Aircraft Equations of Motion

일반적으로 항공기를 표현하는 운동 방정식을 유도할 때 다음과 같은 가정을 따른다.

• 지면 좌표계를 관성 좌표계로 가정한다.
• 항공기의 탄성 변형이 없는 강체로 가정한다.
• 항공기의 질량 변화나 분포의 변화가 없다고 가정한다.

강체로 이루어진 물체의 운동은 3차원 공간에서의 X축, Y축, 그리고 Z축에 대한 선형 이동(Translation)과 회전 이동(Rotation)을 모두 고려하면 6자유도(6 Degree-of-Freedom)를 갖게 된다. 따라서 일반적인 강체의 운동방정식을 6자유도 운동방정식이라고 부른다.

그래서, 선형 이동을 표현하는 선형 운동 방정식과 회전 이동을 표현하는 회전 운동 방정식을 차례대로 도출하려고 한다.

Law of Conservation of Linear Momentum

관성좌표계에 대해서 뉴턴의 제 2 법칙을 기반으로 선형 운동량(Momentum) 보존법칙과 회전 운동량 보존법칙은 다음과 같이 표현된다.

\[\Sigma F_i = \frac{d}{dt} (m v_p) \tag{1}\] \[\Sigma M_i = \frac{d}{dt} (H) \tag{2}\]

여기서, $v_p$는 관성좌표계에 대한 질량중심의 속도 벡터이며, 선형 운동량 보존법칙은 관성좌표계에서만 적용 가능하다.

또한, 이 식은 아래와 같은 의미를 가진다.

• “항공기의 선형 운동량의 시간 변화율은 항공기에 작용하는 외력의 총합과 같다.”

Equation of Linear Motion

Aircraft frame, Inertial Coordinate System

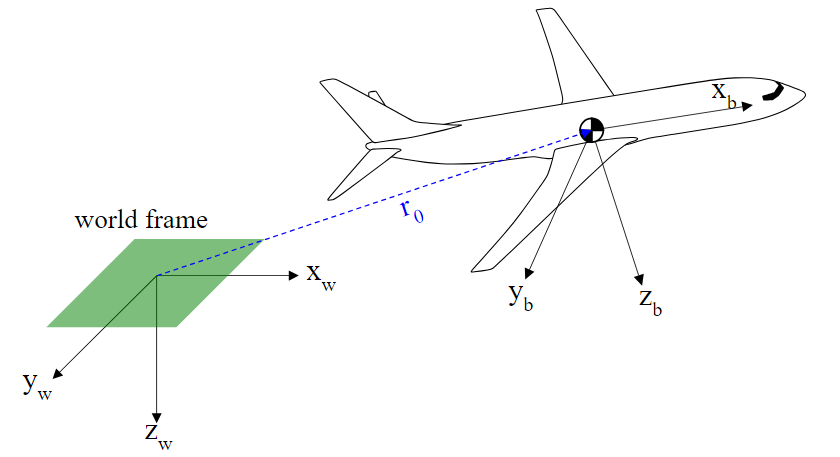
항공기에 고정되어 있는 기체 고정 좌표계의 중심은 비행기의 질량중심(Center of mass)이다.
항공기 질량중심의 움직임은 관성좌표계에 대해 정의된 위치 벡터 $r_p$로 표현이 가능하며, 관성좌표계에 대한 질량중심의 위치 벡터 $r_p$의 시간 변화율로 정의된 속도 벡터 $v_p$는 다음과 같다.

\[v_p = \frac{d r_p}{dt} \tag{3}\]

항공기에 작용하는 공기역학적 힘, 추진기관에 의한 힘, 그리고 중력에 의한 힘(외력)을 고려하면 항공기 질량중심의 선형이동에 대한 운동방정식은 다음과 같이 된다.

\[m \frac{dv_p}{dt} = \Sigma F_i = mg + F_A + F_T \tag{4}\]

여기서 $F_A$는 공기역학적인 힘에 의해 항공기에 작용하는 전체 힘 벡터, $F_T$는 추진기관에 의해 항공기에 작용하는 전체 힘 벡터, 그리고 g는 중력가속도 벡터이다.

임의의 위치 벡터 $r$을 관성좌표계에 대해 미분한 양과 관성좌표계에 대해 회전 각속도 $\omega$로 움직이고 있는 기체 고정 좌표계에 대한 미분과의 관계식은 다음과 같다.

\[\frac{dr}{dt} = \frac{\delta r}{\delta t} + \omega \times r \tag{5}\]

이렇게 되는 과정을 설명해보자면, 관성좌표계에서는 $\frac{d\hat{i}}{dt} = \frac{d\hat{j}}{dt} = \frac{d\hat{k}}{dt} = 0$이기에 식 (7)과 같이 표현되고,
회전좌표계에서는 $\frac{d\hat{i}}{dt} = \frac{d\hat{j}}{dt} = \frac{d\hat{k}}{dt} \neq 0$ 이기에 회전 축이 그대로 남아 식 (8)과 같이 표현된다.

\[\frac{d}{dt}\left( x \hat{i} + y \hat{j} + z \hat{k} \right) = \frac{d}{dt} \left( x' \hat{i'} + y' \hat{j'} + z' \hat{k'} \right) \tag{6}\] \[\frac{d}{dt} \left( x \hat{i} + y \hat{j} + z \hat{k} \right) = \frac{dx}{dt} \hat{i} + \frac{dy}{dt} \hat{j} + \frac{dz}{dt} \hat{k} + x \frac{d\hat{i}}{dt} + y \frac{d\hat{j}}{dt} + z \frac{d\hat{k}}{dt} = \frac{dx}{dt} \hat{i} + \frac{dy}{dt} \hat{j} + \frac{dz}{dt} \hat{k} = \vec{v} \tag{7}\] \[\frac{d}{dt} \left( x' \hat{i'} + y' \hat{j'} + z' \hat{k'} \right) = \frac{dx'}{dt} \hat{i'} + \frac{dy'}{dt} \hat{j'} + \frac{dz'}{dt} \hat{k'} + x' \frac{d\hat{i'}}{dt} + y' \frac{d\hat{j'}}{dt} + z' \frac{d\hat{k'}}{dt} \tag{8}\] \[\vec{v'} = \frac{dx'}{dt} \hat{i'} + \frac{dy'}{dt} \hat{j'} + \frac{dz'}{dt} \hat{k'} \tag{9}\] \[\boldsymbol{\omega} \times \vec{r'} = x' \frac{d\hat{i'}}{dt} + y' \frac{d\hat{j'}}{dt} + z' \frac{d\hat{k'}}{dt} \tag{10}\] \[\vec{v} = \vec{v'} + \boldsymbol{\omega} \times \vec{r'} \tag{11}\]

여기서 $d/dt$는 고정좌표계에 대한 시간미분을, $\delta/\delta t$는 회전좌표계에 대한 시간미분을 의미한다. 항공기에 고정되어 있는 기체 고정 좌표계 $X_b, Y_b, Z_b$가 관성좌표계에 대해 각속도 $\omega$벡터로 회전하고 있다고 가정하면, 항공기 질량중심의 선형이동에 대한 운동방정식은 다음과 같이 쓸 수 있다.

\[m \left( \frac{\delta v_p}{\delta t} + \omega \times v_p \right) = mg + F_A + F_T \tag{12}\]

이러한 과정이 필요한 이유는 기체 고정 좌표계는 비관성 좌표계이기 때문에 회전 효과를 고려해야 한다는 점 때문이다. 회전 좌표계에서는 코리올리 효과와 원심력과 같은 추가적인 관성력이 발생하므로, 이를 반영하여 물체의 운동을 정확하게 설명할 필요가 있다.
관성 좌표계에서의 시간 미분을 사용할 경우, 회전 효과가 반영되지 않으므로, $\frac{\delta v_p}{\delta t}$ 항에 각속도 벡터 $\omega$에 의한 추가 항인 $\omega \times v_p$를 더하여 기체 고정 좌표계에서의 정확한 운동을 설명할 수 있다.

항공기 무게중심의 선형속도, 각속도, 중력가속도, 공기역학적 힘, 그리고 추력에 의한 힘의 성분들은 기체 고정 좌표계의 $X_b$, $Y_b$, $Z_b$ 축을 기준으로 다음과 같이 정의된다.

\[v_p = U \hat{i} + V \hat{j} + W \hat{k} \tag{13}\] \[\omega = P \hat{i} + Q \hat{j} + R \hat{k} \tag{14}\] \[g = g_x \hat{i} + g_y \hat{j} + g_z \hat{k} \tag{15}\] \[F_A = F_{Ax} \hat{i} + F_{Ay} \hat{j} + F_{Az} \hat{k} \tag{16}\] \[F_T = F_{Tx} \hat{i} + F_{Ty} \hat{j} + F_{Tz} \hat{k} \tag{17}\]

앞의 정의를 이용해서 다음과 같은 관계식을 얻을 수 있다.

\[\frac{\delta v_p}{\delta t} = \dot{U} \hat{i} + \dot{V} \hat{j} + \dot{W} \hat{k} \tag{18}\] \[\omega \times v_p = (-VR + WQ) \hat{i} + (UR - WP) \hat{j} + (-UQ + VP) \hat{k} \tag{19}\]

이제, 선형 운동량 보존법칙으로 유도된 운동방정식을 성분별로 정리하면 다음과 같다.

\[m \left( \dot{U} - VR + WQ \right) \hat{i} + \left(\dot{V} + UR - WP \right) \hat{j} + \left( \dot{W} - UQ + VP \right) \hat{k} = mg + F_A + F_T \tag{20}\]

마지막으로, 항공기의 각 축($X_b$, $Y_b$, $Z_b$)에 대한 성분별로 선형 운동 방정식을 유도하면 다음과 같다.

\[m \left( \dot{U} - VR + WQ \right) = mg_x + F_{Ax} + F_{Tx} \tag{21}\] \[m \left( \dot{V} - WP + UR \right) = mg_y + F_{Ay} + F_{Ty} \tag{22}\] \[m \left( \dot{W} - UQ + VP \right) = mg_z + F_{Az} + F_{Tz} \tag{23}\]

다음 포스트에서는 이어서 회전 운동 방정식에 대해 설명하려고 한다.