[Flight Control 3] - Aircraft Coordinate Transformations
Aircraft Coordinate Transformations
항공기의 자세를 지구에 대해 나타내기 위해서는, 기체 고정 좌표계 $X$ $Y$ $Z$(=$X_B$, $Y_B$, $Z_B$)를 지면 좌표계에 대해 표시하여야 한다.
우선, 지면 좌표계의 원점이 비행기의 중심 P와 일치하도록 평행 이동하였다고 하자.
이를 $X_1$,$Y_1$,$Z_1$이라고 하고,$Z_1$축에 대해서 요각 만큼 회전한 좌표계를 $X_2$,$Y_2$,$Z_2$,$Y_2$축에 대해서 피치각 만큼 회전한 좌표계를 $X_3$,$Y_3$,$Z_3$이라고 한다.
그리고 다시 $X_3$축에 대해서 롤각 만큼 회전한 좌표계를 $X$ $Y$ $Z$라하자.
이러한 좌표계 변환을 $3-2-1$ 변환이라고 하며, 이때 정의된 요각, 피치각, 롤각을 오일러각이라고 한다.
Direction Cosine Matrix (DCM)
Yaw($\psi$) Rotation
Yaw Rotation
이와 같이 정의된 오일러각을 이용하여 기체 고정 좌표계에서 표시한 벡터 $(U, V, W)$와 지면 좌표계에서 표시한 $(U_1, V_1, W_1)$의 관계식을 유도한다.
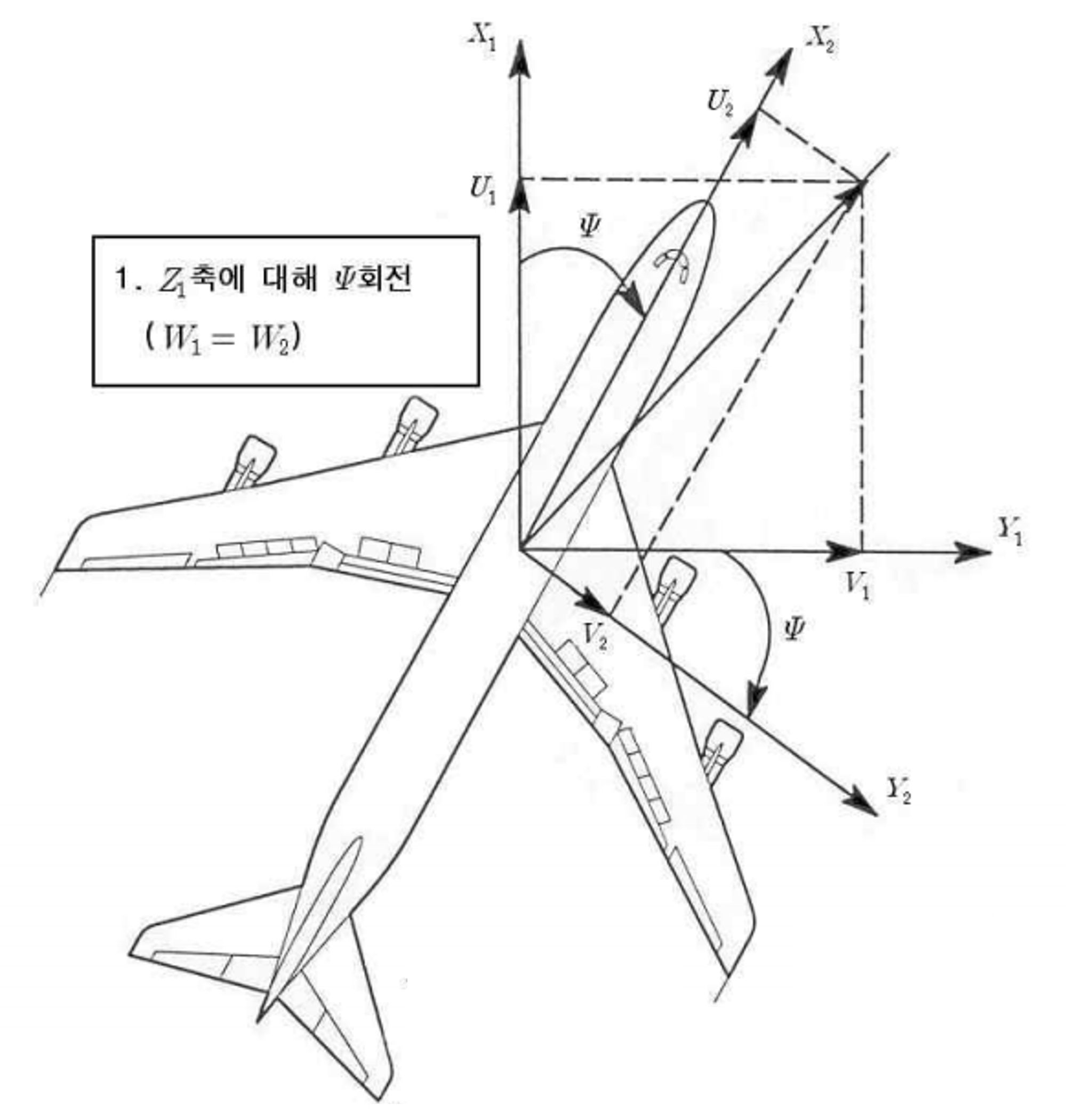
지면 좌표계와 일치하는 좌표계 $(X, Y, Z)$를 $Z_1$축에 대해서 요각 만큼 회전하여 $X_2, Y_2, Z_2$를 얻었다고 하였다.
$X_2, Y_2, Z_2$좌표계에서 표시한 벡터성분을 $(U_2, V_2, W_2)$라 하면 다음 관계가 성립한다.
Pitch($\theta$) Rotation
Pitch Rotation
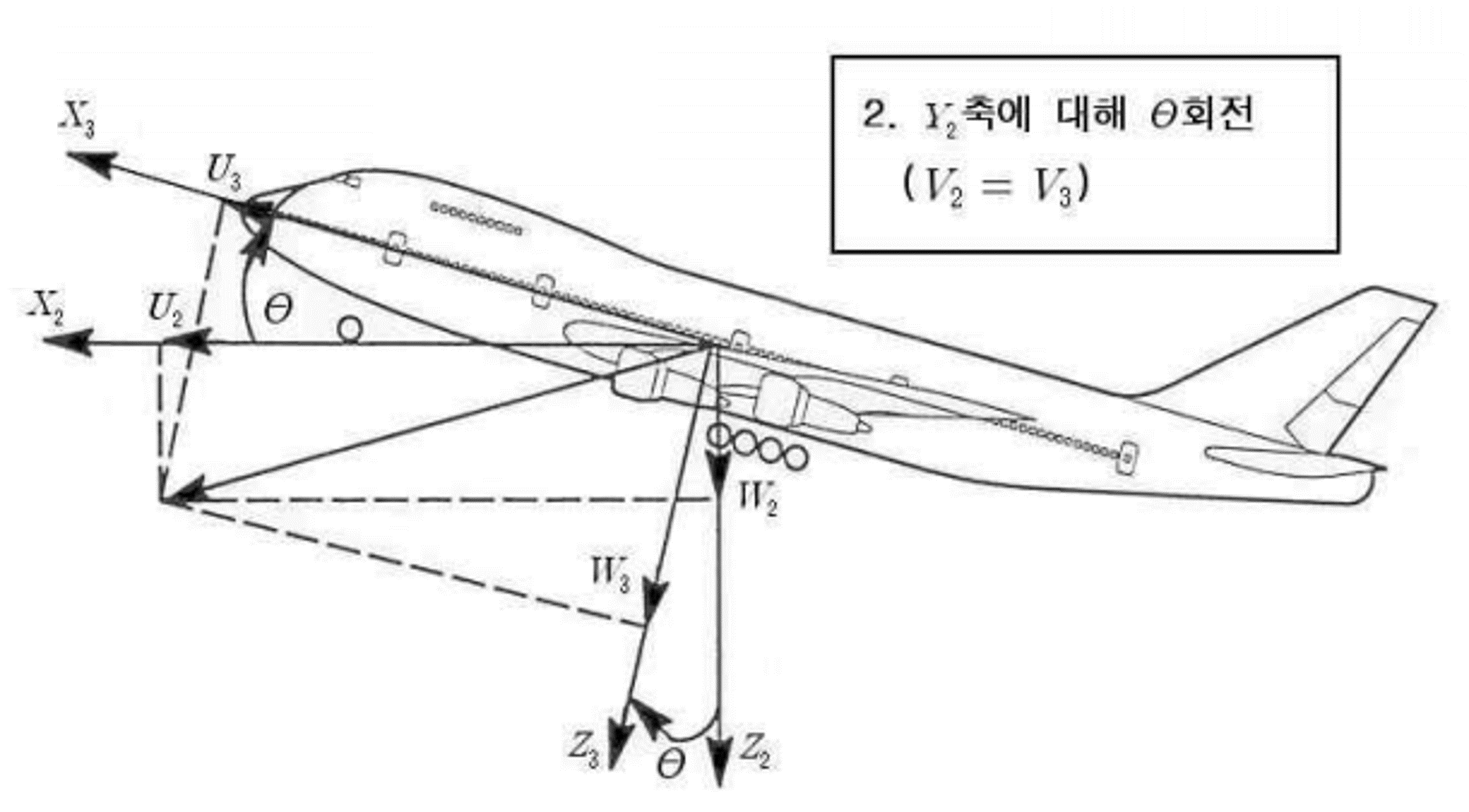
이제 $X_2, Y_2, Z_2$ 좌표계를 $Y_2$ 축에 대해서 피치각 만큼 회전한 좌표계를 $X_3, Y_3, Z_3$라 하였다. $X_3, Y_3, Z_3$ 좌표계에서 표시한 벡터성분을 $(U_3, V_3, W_3)$라 하면 다음 관계가 성립한다.
\[\begin{aligned} U_3 &= U_2 \cos \Theta - W_2 \sin \Theta \\ V_3 &= V_2 \\ W_3 &= U_2 \sin \Theta + W_2 \cos \Theta \end{aligned} \tag{3}\] \[\begin{pmatrix} U_3 \\ V_3 \\ W_3 \end{pmatrix} = \begin{bmatrix} \cos \Theta & 0 & -\sin \Theta \\ 0 & 1 & 0 \\ \sin \Theta & 0 & \cos \Theta \end{bmatrix} \begin{pmatrix} U_2 \\ V_2 \\ W_2 \end{pmatrix} \equiv \Theta \begin{pmatrix} U_2 \\ V_2 \\ W_2 \end{pmatrix} \tag{4}\]Roll($\phi$) Rotation
Roll Rotation
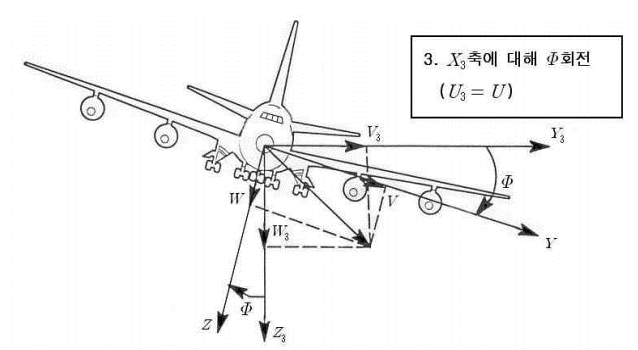
끝으로 $X_3, Y_3, Z_3$ 좌표계를 $X_3$ 축에 대해서 롤각 만큼 회전한 좌표계가 기체 고정 좌표계 $XYZ$이고, 기체 고정 좌표계에서 표시한 벡터성분이 $(U, V, W)$이므로 다음 식이 성립한다.
\[\begin{aligned} U &= U_3 \\ V &= V_3 \cos \Phi + W_3 \sin \Phi \\ W &= -V_3 \sin \Phi + W_3 \cos \Phi \end{aligned} \tag{5}\] \[\begin{pmatrix} U \\ V \\ W \end{pmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \Phi & \sin \Phi \\ 0 & -\sin \Phi & \cos \Phi \end{bmatrix} \begin{pmatrix} U_3 \\ V_3 \\ W_3 \end{pmatrix} \equiv \Phi \begin{pmatrix} U_3 \\ V_3 \\ W_3 \end{pmatrix} \tag{6}\]위 식들을 아래와 같이 정리할 수 있다.
\[\begin{pmatrix} U \\ V \\ W \end{pmatrix} = \Phi \Theta \Psi \begin{pmatrix} U_1 \\ V_1 \\ W_1 \end{pmatrix} \equiv C \begin{pmatrix} U_1 \\ V_1 \\ W_1 \end{pmatrix} \tag{7}\]이때의 좌표변환행렬 C는 Direction Cosine Matrix (DCM)이라고 하며, 지면 좌표계에서 기체 고정 좌표계로 변환을 진행하게 된다.
\[C = \begin{bmatrix} \cos \Psi \cos \Theta & \sin \Psi \cos \Theta & -\sin \Theta \\ -\sin \Psi \cos \Phi + \cos \Psi \sin \Theta \sin \Phi & \cos \Psi \cos \Phi + \sin \Psi \sin \Theta \sin \Phi & \cos \Theta \sin \Phi \\ \sin \Psi \sin \Phi + \cos \Psi \sin \Theta \cos \Phi & -\cos \Psi \sin \Phi + \sin \Psi \sin \Theta \cos \Phi & \cos \Theta \cos \Phi \end{bmatrix} \tag{8}\]또한, $C$는 표준직교(Orthonormal)행렬로 기체 고정 좌표계의 성분에서 지면 좌표계의 성분으로 변환시키기 위하여 식 (9) 와 같이 표현 할 수 있다.
\[\begin{pmatrix} U_1 \\ V_1 \\ W_1 \end{pmatrix} = \Psi^T \Theta^T \Phi^T \begin{pmatrix} U \\ V \\ W \end{pmatrix} \equiv [C]^T \begin{pmatrix} U \\ V \\ W \end{pmatrix} \tag{9}\]